Wer das von Michael Klein und Dr. habil. Heike Diefenbach betriebene Wissenschaftsblogsatireblog ScienceFiles: Kritische Wissenschaft - critical science für eine jener nicht weiter beachtenswerten Kuriositäten hält, die einem das Internet nunmal in großer Fülle beschert, den werde ich von dieser Meinung nicht abbringen wollen. Jedoch muß man anerkennen, daß dieses Blog Beachtliches leistet; so habe ich erst durch diesen Artikel erfahren, daß das Ziegenproblem ein Problem der Ziegen ist, und daß ein Kakerlakenproblem niemals ein Grund sein kann, den Kammerjäger zu rufen, sondern bestenfalls der Kammerjäger selbst, und das ist erst der Anfang der erstaunlichen Einsichten, die in diesem Artikel dargeboten werden, und denen einen eigenen Artikel zu widmen ich aus Angst, mich totzulachen, scheue. Wer die nötige Indolenz mitbringt, der kann also aus den Anhäufungen von Invektiven, die auf ScienceFiles erscheinende Artikel in aller Regel hauptsächlich darstellen, bisweilen doch noch die eine oder andere nachprüfbare Aussage extrahieren und sich durch Bestimmung ihres Wahrheitswertes einen amüsanten Zeitvertreib schaffen.
Zudem muß berücksichtigt werden, daß es Texte dieses Blogs inzwischen auch in Schulbücher schaffen - ob als abschreckendes Beispiel oder was auch immer.
Des Weiteren hat ScienceFiles bei einer Wahl zum Wissenschaftsblog 2013 den zweiten Platz nach Astrodictium Simplex errungen. Da Astrodictium Simplex im Vergleich mit ScienceFiles, meinem Eindruck nach, zwei große Mängel aufweist, nämlich sich mit Wissenschaft zu beschäftigen und nicht in jedem Beitrag Leuten mit von der eigenen verschiedener Meinung eine Krankheit zu diagnostizieren, dürfte ScienceFiles aus dieser Wahl auch bald als die unangefochtene Nummer eins hervorgehen. Es lohnt sich also möglicherweise, die Qualitäten und Defizite dieser Publikation etwas näher zu betrachten.
Tinnitusgleich schwingen bei der Lektüre des Blogs mantrahaft wiederholte Lippenbekenntnisse zur wissenschaftlichen Methode mit. Der eingangs angesprochene Artikel könnte dabei bereits zu einer Vermutung über die dort vorherrschende Auffassung davon, wie diese Methode anzuwenden sei, verleiten: Etwas nachweislich oder gar offensichtlich falsches behaupten und darauf warten, daß es in den Kommentaren jemand falsifiziert, was angesichts der Qualität des Kommentatorenstammes gemeinhin lange dauert, falls es denn überhaupt je passiert. Nun sind aber Leute, die meinen, sich zu sprachwissenschaftlichen Fragen sachkundig äußern zu können, weil sie mal ein Buch gelesen und eine Pizza bestellt haben und außerdem noch ein Blog betreiben, nicht gerade die seltenste Plage in den Internets, übertroffen nur noch von Leichtathleten, die sich ihrer Kenntnisse der klassischen Mechanik rühmen und Köchen und Bäckern, die sich ja grundsätzlich für Koryphäen auf dem Gebiet der Thermodynamik halten. Vielleicht also hat man sich in diesem Fall bei ScienceFiles nur über Gebühr aus dem Fenster gelehnt, da dies so üblich und schön ist, tappt jedoch durch heimische Gefilde festen und sicheren Schrittes - etwa wenn es um die Anwendung statistischer Methoden geht? Das kann ich nicht mit Sicherheit sagen, habe aber gewisse Zweifel, die ich im Folgenden begründen möchte.
Ein statistisches Artefakt betritt die Bühne
In einem wenig beachteten Artikel vom 25.10. 2013 wird die These aufgestellt, daß die gängigen Messungen relativer Armut und Armutsgefährdung ein Verfahren seien,
um eine funktionale Unterschicht zu schaffen, die egal, wie sich die Gesellschaft entwickelt, nie weggehen wird, denn es wird immer rund ein Sechstel der Bevölkerung geben, das weniger als 60% des Medianeinkommens zur Verfügung hat.
Sinn dieser Übung soll es unter anderem sein, Sozialdienstleistern ein Auskommen zu verschaffen, denn diese bräuchten ja eine Unterschicht, um die sie sich kümmern können. Wenn man es also so einrichtet, daß immer ein Sechstel der Bevölkerung armutsgefährdet ist, muß einem in dieser Hinsicht nicht bange sein, und
[d]ass dem so ist, erklärt sich über die statistische Normalverteilung des Einkommens.
Wie es sich darüber erklärt, wird nicht näher erläutert; die gemeinte Erklärung muß man sich also zusammenraten, etwa auf dieser Grundlage:
Man könnte die Einkommensverteilung fünfteln, so dass dann, wenn man einen Normalverteilung zu Grunde legt rund 20% in Armut leben, was erreicht ist, wenn man den Schnittpunkt bei 75% des Median-Einkommens oder, wie es so schön heißt, des Nettoäquivalenzeinkommens setzt.
Man kann jetzt immerhin ein Muster erkennen: Wie unterhalb von 60% des Medianeinkommens immer rund ein Sechstel der Bevölkerung zu finden sein soll, so soll es unterhalb von 75% rund ein Fünftel davon sein, und dies soll ausschließlich auf die Normalverteilung des Einkommens zurückzuführen sein. Wir kommen darauf später zurück.
Die These lautet also: Der Anteil der Armutsgefährdeten ist "ein statistisches Artefakt", also etwas, das sich aus mathematischen Gründen einstellen muß, solange Einkommen normalverteilt ist, was es nunmal ist, und folglich ohne jeden empirischen Gehalt. Da die Praxis, Menschen mit einem Einkommen1 unterhalb von 60% des Medianeinkommens als armutsgefährdet auszuweisen, sich in ganz Europa und darüber hinaus großer Beliebtheit erfreut, wäre dies natürlich ein Ergebnis, daß größte Aufmerksamkeit verdient hätte, wenn es denn stimmte. Was es aber natürlich nicht tut.
Exkurs: Normalverteilung
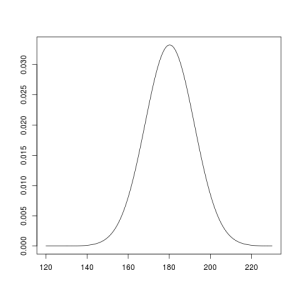
Was es bedeutet, wenn der Wert einer bestimmten Zufallsgröße normalverteilt ist, wie es beispielsweise für die Körpergröße der Fall ist, kann man sich etwa wie folgt vorstellen: Man greife eine große Zahl von Leuten zufällig aus der Bevölkerung heraus und weise sie an, sich in Reihen aufzustellen, wobei in jede Reihe genau die Leute kommen, deren Körpergröße in einem bestimmten Intervall, z.B. 185-189cm, liegt (und auch tatsächlich jede Körpergröße zu irgendeiner Reihe gehört). Dann wird sich, wenn man die Reihen nach aufsteigender Körpergröße sortiert, von oben betrachtet ein Muster ergeben, um das sich recht gut passend eine sogenannte Glockenkurve wird legen lassen, wie sie die folgende Graphik am Beispiel der männlichen Körpergröße illustriert.2
Sehr schön sehen kann man das hier, wo ebenfalls nach Geschlecht getrennt wird und man gut die Andeutung zweier gegeneinander verschobener Glockenkurven, jeweils eine für die männliche und eine für die weibliche Größe, erkennt.
Die Glockenkurve ist der Graph der zur Normalverteilung gehörenden Dichtefunktion. Der Wert, an dem die Dichte am höchsten ist (ca. 180cm in obiger Graphik) ist der sogenannte Median. Der Median teilt die Fläche unterhalb der Kurve in zwei gleiche Hälften. Die Gesamtfläche unterhalb der Kurve hat stets die Größe 1, und bestimmt man den Flächeninhalt eines bestimmten Teils dieser Fläche, etwa des Teils über dem Intervall von 170cm bis 180cm, in der folgenden Graphik gelb markiert, so erhält man die Wahrscheinlichkeit, daß die Körpergröße eines zufällig aus der beschriebenen Gesamtheit herausgegriffenen Mannes innerhalb dieses Intervalls liegt. (Das sind in unserem Fall etwa 43,6%.)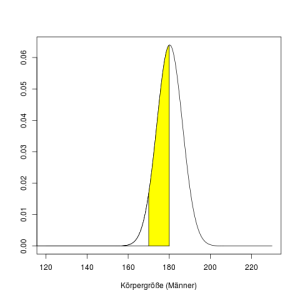
Die genaue Form der Glockenkurven hängt von der zugrundeliegenden Standardabweichung ab, deren Quadrat die sogenannte Varianz ist. Je größer die Varianz, desto größer ist die Abweichung vom Median, die man bei einer zufälligen Messung (also etwa der Körpergröße eines zufällig ausgewählten Mannes) erwarten darf. Im Fall der oben gezeigten Glockenkurve liegt der Median bei etwa 180cm und die Standardabweichung etwa bei 6cm. Durch diese beiden Parameter ist die Kurve eindeutig bestimmt. Mit einer Standardabweichung von 12cm sähe die Kurve so aus, also deutlich breiter:
Um die These des ScienceFiles-Artikels zu widerlegen, muß man mehr nicht wissen.
Das statistische Artefakt geht wieder ab
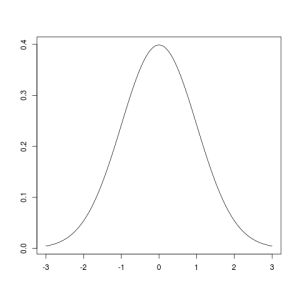
Ob das Einkommen wirklich normalverteilt ist, was von Kommentatoren des Beitrags auf ScienceFiles bereits in Zweifel gezogen wurde, muß uns hier nicht interessieren, denn die dort aufgestellte Behauptung ist auch dann falsch, wenn es das ist. Man sieht das ganz leicht, wenn man etwa die Standardnormalverteilung als Beispiel nimmt:
Deren Median ist gleich 0 (die Standardabweichung beträgt 1), und gälte die postulierte Gesetzmäßigkeit uneingeschränkt, so müßten unterhalb von 60% des Medians wieder etwa 16% der Gesamtheit liegen. Da 0,6×0=0 sind 60% des Medians mit dem Median identisch, und da unter dem Median nach Definition immer 50% der Gesamtheit liegen, wäre demnach 0,16=0,5, was hoffentlich nicht der Fall ist.
Etwas konkreter verdeutlichen Bilder, was von der Behauptung zu halten ist. Ich betrachte jetzt Verteilungen mit positivem Median, z.B. also Einkommensverteilungen.3 Dabei nehme ich der Einfachheit halber ein Medianeinkommen von 100 Talern an, der Trick funktioniert aber mit allen positiven Zahlen und allen Währungen. In den folgenden Graphiken entspricht der rot markierte Teil demjenigen Teil der Gesamtheit, dessen Einkommen unterhalb von 60% des Medians, also 60 Talern, liegt. Der gelb markierte Teil entspricht, im Verein mit dem rot markierten, dem Teil der Gesamtheit, dessen Einkommen unterhalb von 75% des Medians liegt. Die Standardabweichung beträgt in diesem Beispiel 41,6 Taler.

Der rote Teil füllt dabei ziemlich genau 16% der Fläche unterhalb der Kurve aus, der rote und gelbe zusammen gut 26,5% (nicht rund 20%, wie auf ScienceFiles behauptet, wenn man nicht äußerst großzügig rundet).
Im folgenden Beispiel wurde die Standarabweichung auf 20 Taler heruntergesetzt. Es fällt ins Auge, daß die Größen der farbigen Flächen sich im Vergleich zur vorangegangenen Graphik, auch hinsichtlich ihres Anteils an der Gesamtfläche unter der Kurve, deutlich verändert haben.
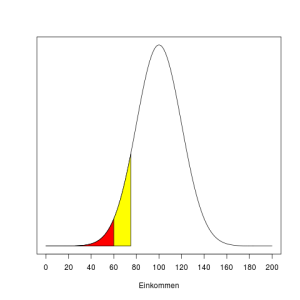
Tatsächlich füllen der gelbe und der rote Bereich gemeinsam nur noch etwa 10,5% der Fläche; der Rote alleine ist auf rund 2,3% geschrumpft. Das ist auch nicht so richtig überraschend, besagt es doch bloß, daß es - Normalverteilung vorausgesetzt - umso weniger Arme gibt, je niedriger die Einkommensungleichheit ist, wenn wir darunter der Einfachheit halber mal die Varianz der Einkommensverteilung verstehen wollen, wogegen nichts zu sprechen scheint.4
Nachtrag: Wenn man die Behauptung auf die Körpergröße überträgt, so besagt sie, daß rund 16% aller Männer kleiner als 1,08 Meter sind. Das allein sollte schon zu denken geben.
Damit ist bereits eindeutig gezeigt, daß die Behauptung von ScienceFiles sich nicht halten läßt. Aber wie kommt man überhaupt darauf? Das war mir zunächst ein Rätsel, und eine mögliche Antwort auf diese Frage ist mir erst vor Kurzem eingefallen.
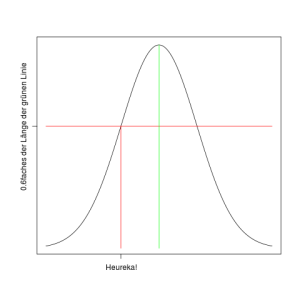
Da sich unter Benutzung der vorgesehenen 60% des Medianeinkommens kein Blumenkohl gewinnen läßt, könnte man sich nach einer Alternative zum Medianeinkommen umsehen und eben halt irgendwie mal so 60% von dieser nehmen. Damit es psychologisch gelingt, diese Alternative auch für den Median zu halten, sollte sie sich so einfach und direkt wie möglich aus diesem ergeben, und dafür bietet sich die Dichte des Medians, also die Höhe des höchsten Punktes der Glockenkurve, hervorragend an. Nun ist die Dichte des Medians natürlich kein Einkommen. Aber man kann auf ihrer Grundlage ein Einkommen bestimmen, z.B. indem man den kleineren der beiden Einkommenswerte nimmt, deren Dichte das 0,6fache der Mediandichte beträgt.
Der so gefundene Punkt ist in der Graphik mit "Heureka!" beschriftet. Irgendeine notwendige Beziehung zu den gewünschten 60% des Medianeinkommens hat er zwar nicht. Dafür hat er die tolle Eigenschaft, daß sich unterhalb seiner immer 15,6% - also hinreichend ungefähr 16% - der Gesamtheit finden. D.h. dies gilt jetzt völlig unabhängig von Median und Standardabweichung der vorliegenden Normalverteilung. Im Fall der ersten oben gezeigten Einkommensverteilung fällt der Punkt ungefähr mit 60% des Medianeinkommens zusammen. Bestimmt man ihn jedoch für die zweite Verteilung, so entspricht er rund 80% des Medianeinkommens. Je kleiner die Standardabweichung wird, desto größer wird dieser Prozentsatz.
Dafür, daß diese Idee der Behauptung im Artikel tatsächlich zugrunde liegt, spricht das Folgende: Bestimmt man einen Punkt in entsprechender Weise für 75% der Dichte des Medians, so ergibt sich in gleicher Weise, daß sich unterhalb dieses Punktes etwa 22%, etwas gröber also rund 20%, der Gesamtheit finden. Auch dieser Wert entspricht also leidlich genau dem auf ScienceFiles genannten. Auch dieser Wert steht selbstverständlich in keiner notwendigen Beziehung zu dem, den man für 75% des Medianeinkommens erhält.5
Ein überraschendes Fazit
Ich weiß nicht, was man von Sozialwissenschaftlern im Allgemeinen erwarten kann und was nicht, bin mir aber sicher, daß die meisten in der Lage sind, eine Zahl mit 0,6 zu multiplizieren, wenn man ihnen einen Taschenrechner und etwas Zeit gibt.6 Sollte der besprochene Artikel also repräsentativ sein für die mathematisch-statistischen Skills, die man von ScienceFiles erwarten darf, so wäre dem Blog zu raten, sich anstelle solcher Übungen künftig gänzlich auf groteske Behauptungen zur Semantik deutscher Komposita zu beschränken. Einfach deshalb, weil es damit im Schnitt weniger Schaden anrichten dürfte.
Anmerkungen
Genauer: Nettoäquivalenzeinkommen. ↩
Die zugrundeliegenden Daten habe ich ohne Prüfung aus einem online stehenden Statistikpräsentation übernommen. Da die Daten nur der Illustration dienen, kommt es auf die exakten Werte nicht an. ↩
Die Kurven werden beim Einkommenswert 0 abgeschnitten, was der These entspricht, daß es kein negatives Einkommen gebe. Man sieht leicht ein, daß dieser Umstand für die Argumentation völlig unerheblich ist. ↩
"relative poverty is a measure of income inequality"; Wikipedia ↩
Alternativ könnte man die Behauptung ableiten, indem man postuliert, daß die Standardabweichung einer Einkommensverteilung immer etwa das 0,4fache des Medians betragen muß, denn mehr als eine Standardabweichung unterhalb des Medians finden sich stets rund 15,86% der Gesamtheit. Eine solche Gesetzmäßigkeit wird auf ScienceFiles jedoch nirgends behauptet, schon gar nicht begründet und ist auch keinesfalls offensichtlich. Aus dem Vorliegen einer Normalverteilung alleine ergibt sie sich, wie gesehen, auf jeden Fall nicht. Nachtrag: Das garantiert das gewünschte Ergebnis allerdings nur für die 60%-Marke. Unterhalb von 75% finden sich dann stets, wie oben gesehen, etwa 26,5% ↩
Sorry dafür. ↩